Sila a pohyb

Silou a pohybom sa zaoberá mechanika, ktorá je považovaná za kľúčovú oblasť fyziky. Je možné tvrdiť, že všetko vo vesmíre sa pohybuje. Môže ísť aj len o veľmi drobný pohyb a veľmi, veľmi pomalý pohyb, ale deje sa. Fyzika pohybu sa zaoberá najmä silami. Ak chceme spôsobiť pohyb objektu alebo zmeniť jeho pohyb, potrebujeme na objekt pôsobiť silou. Žiadna zmena pohybu sa nedeje sama od seba, vždy ide o zmenu pôsobenia síl na daný objekt. Zmena pôsobenia síl na objekt môže spôsobiť zmenu smeru jeho pohybu a/ alebo zmenu rýchlosti jeho pohybu.

Rýchlosť, zrýchlenie, hmotnosť a hybnosť pohybujúceho sa objekt

Pri zmene pohybu je potrebné brať do úvahy rýchlosť, zrýchlenie a hmotnosť objektu. Rýchlosť objektu vyjadruje to, akú dráhu objekt prejde za určitý čas. Zrýchlenie vyjadruje to, ako sa zväčšila rýchlosť pohybu objektu za určitý čas. Pohyb objektov závisí aj od ich hmotnosti. Hmotnosť vyjadruje množstvo materiálu, ktorým je objekt tvorený (vyjadruje sa v kilogramoch, gramoch). Takže napríklad pohybujúce sa auto má určitú rýchlosť, zrýchlenie a hmotnosť. Tieto vlastnosti je potrebné brať do úvahy pri hodnotení jeho pohybu, najmä pri snahe zmeniť jeho pohyb, napríklad pri snahe auto zastaviť.

Rýchlosť aj zrýchlenie majú vektorový charakter. To znamená, že majú svoju veľkosť aj smerovanie. Najjednoduchšie sa to vysvetľuje na zobrazení pomocou šípok. Šípka určuje smer rýchlosti a jej dĺžka určuje to, ako rýchlo sa objekt v určitom smere pohybuje. Zrýchlenie je tiež vektorová veličina. Objekt zrýchľuje vtedy, keď zrýchlenie aj rýchlosť majú rovnaký smer. Ak majú smer opačný, objekt spomaľuje. Špecifické je tzv. konštantné zrýchlenie. Zrýchlenie je konštantné v prípadoch, kedy na objekt pôsobí konštantná sila. Príkladom konštantného zrýchlenia je tzv. gravitačné zrýchlenie, ktoré je výsledkom pôsobenia konštantnej gravitačnej sily Zeme. Gravitácia pôsobí na objekt konštantnou silou smerom do centra planéty Zem. Gravitačná sila Zeme sa zmenšuje so zväčšujúcou sa vzdialenosťou od povrchu planéty. Tiež je zaujímavé si uvedomiť, že gravitácia iných planét sa od gravitácie Zeme odlišuje, keďže planéty môžu mať väčšiu alebo menšiu hmotnosť ako planéta Zem. Preto predmety pri páde zrýchľujú inak na Zemi a inak na iných planétach.

Ak vynásobíme rýchlosť objektu jeho hmotnosťou, dostaneme ďalšiu vektorovú veličinu – hybnosť. Hybnosť má vždy rovnaký smer ako rýchlosť. V princípe táto veličina vyjadruje to, aké ťažké je zastaviť určitý pohybujúci sa objekt. Ak napríklad beží človek rýchlosťou 10 kilometrov za hodinu a váži 50 kg, jeho hybnosť je 500 kg.m/s. Ak letí lopta, ktorá váži 1 kilogram rýchlosťou 10 kilometrov za hodinu, v prípade, že nás trafí, zraní nás menej ako lopta, ktorá váži viac a/alebo sa pohybuje rýchlejšie. Hybnosť takejto lopty je 10 kg.m/s.

Z uvedeného, okrem iného, vyplýva, že aj veľmi drobné objekty (ľahké) nás môžu zraniť viac ako veľké objekty (ťažké), ak je ich rýchlosť veľmi veľká. Typickým príkladom je náboj vystrelený zo zbrane. Náboj sám o sebe je veľmi ľahký a ak by ho do nás niekto len hodil, tak nám vôbec neublíži. Práve hybnosť spôsobuje zranenia, pričom veľká hybnosť náboja je z nepomerne väčšej časti spôsobená rýchlosťou náboja, nie jeho hmotnosťou. Platí to aj naopak. Aj veľmi pomaly sa pohybujúce, ale ťažké predmety nám môžu ublížiť, napríklad ak si pricvikneme prsty pod skriňu, ktorú sťahujeme.

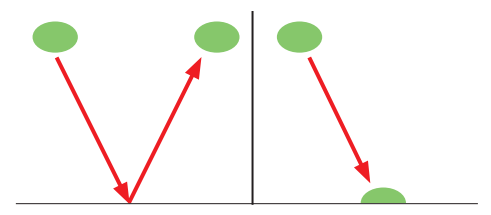
Hybnosť objektu predstavuje kinetickú energiu objektu. Tá sa zachováva aj vtedy, ak takýto objekt narazí na prekážku a odrazí sa od nej. Platí to však len vtedy, ak ide o ideálne pružný objekt. Pri náraze objektu s ideálnou pružnosťou sa mení hybnosť objektu, ale len v smere jej pôsobenia. Veľkosť hybnosti zostáva rovnaká, mení sa len smer, ktorým sa objekt pohybuje. V princípe ideálna pružnosť neexistuje, poznáme len objekty s rôzne veľkou pružnosťou. Čím menej pružný materiál je, tým viac kinetickej energie sa pri odraze stráca. Ideálne pružný a ideálne nepružný dopad objektu a vplyv dopadu na hybnosť sú zobrazené na obrázku. Keďže ideálne pružné a nepružné materiály neexistujú, nie je možné tento jav demonštrovať, je však možné pozorovať rozdiely medzi predmetmi s veľmi vysokou a veľmi nízkou pružnosťou, napríklad pingpongovú loptičku a plastelínu. Ak hodíme na zem guľôčku plastelíny, tá zostane deformovaná ležať na podlahe. Časť kinetickej energie plastelíny sa zmenila na teplo (plastelína sa pádom zahreje) a zvuk (vibrácia na podlahe a zvukové vlny vo vzduchu). Keďže po dopade je rýchlosť nulová, aj hybnosť je nulová. Kinetická energia nezmizla, len sa premenila na inú formu energie. Čím pružnejší je materiál, tým viac energie zostáva vo forme pohybovej energie, napríklad pingpongová loptička sa na rozdiel od plastelíny od prekážky odrazí.

Obrázok 22: Dopad a jeho vplyv na hybnosť

Newtonove tri pohybové zákony

Na základe dlhodobého štúdia pohybu boli postupne definované základné princípy pohybu a zmien v pohybe, ktoré nazývame aj pohybovými zákonmi. Formuloval ich Isaac Newton a sú tri. Okrem týchto základných troch pohybových zákonov poznáme aj ďalšie, ktoré sa viažu na špecifické prípady pohybov, ako je pohyb rýchlosťou blížiacou sa rýchlosti svetla a tiež pohyb v mikrosvete, na úrovni atómov. Z toho vyplýva, že v týchto špecifických situáciách prestávajú Newtonove pohybové zákony platiť.

Prvý pohybový zákon hovorí o tom, že pohybujúci sa objekt zotrváva v pohybe v tom istom smere a tou istou rýchlosťou, kým naň nepôsobí nejaká sila. To znamená, že ak kopneme do lopty, tá bude letieť konštantnou rýchlosťou nekonečne ďaleko, kým na ňu nebude pôsobiť iná sila. Aj napriek tomu, že na prvý pohľad nie je tento zákon v súlade s realitou, platí to absolútne. Po kopnutí do lopty pôsobia na pohybujúcu sa loptu sily, ktoré spôsobujú jej spomaľovanie a následne aj pád. Ide napríklad o gravitačnú silu Zeme, ktorá ťahá loptu smerom dolu (táto sila pôsobí na loptu aj kým leží v pokoji), ale aj trenie o vzduch, v ktorom sa lopta pohybuje.

Druhý pohybový zákon hovorí o tom, že čím väčšiu hmotnosť objekt má, tým väčšiu silu bude potrebné vynaložiť na to, aby sa pohyb objektu zrýchlil (F = m.a). Okrem iného to znamená, že čím silnejšie kopnete do lopty, tým ďalej bude letieť. Ak teda pôsobíme rovnakou silou na dva objekty s rôznou hmotnosťou, viac zrýchli objekt, ktorý má väčšiu hmotnosť.

Tretí pohybový zákon hovorí o tom, že každá akcia vyvoláva rovnako veľkú, ale opačne pôsobiacu reakciu. To znamená, že v každom momente existujú dve sily vzájomne na seba pôsobiace. V príklade s loptou to znamená, že keď vynaložíme silu na kopnutie do lopty, tak aj lopta pôsobí rovnako veľkou silou na našu nohu, len opačným smerom. Cítime to najmä vtedy, keď do lopty kopneme prstami. Sila, ktorou lopta pôsobí na našu nohu môže byť taká veľká (závisí od toho, ako silno do lopty kopneme), že spôsobí zlomenie prsta. Viditeľnejšie sa tretí pohybový zákon prejavuje napríklad pri strieľaní z dela (ale aj z iných strelných zbraní). Výbuchom je dodaná sila delovej guli, ktorá je kanónom v určitom smere vystrelená. Avšak rovnako veľkou silou pôsobí aj delová guľa na kanón. Kanón sa pohne opačným smerom ako vystrelená delová guľa, nie však tak rýchlo ako samotná guľa a to preto, lebo kanón je oveľa ťažší a na jeho zrýchlenie je preto potrebné vynaložiť väčšiu silu, ako na zrýchlenie oveľa ľahšej delovej gule.

Jednoduchý a zložený pohyb

Existujú dva pohľady na výsledný, pozorovaný pohyb objektov. Prvý pohľad rieši pohyb ako priamočiare premiestňovanie, pričom rýchlosť premiestňovania môže byť konštantná, ale vplyvom síl pôsobiacich v smere pohybu alebo v presne opačnom smere sa môže objekt pohybovať pomalšie alebo rýchlejšie. Zložitejším je pohyb, pri ktorom objekt mení smer svojho pohybu. Napríklad rotujúce objekty alebo lopta hodená šikmým vrhom. Aj pri takýchto pohyboch musí na objekt pôsobiť sila, avšak tá pôsobí nie v smere pohybu objektu (prípadne proti smeru pohybu), ale pod určitým uhlom.

Aktívna a uskladnená energia

Na vysvetlenie toho, prečo sa veci okolo nás dejú tak, ako sa dejú, používame pojem energia. Poznáme rôzne formy energie, napríklad slnečnú, atómovú, elektrickú, chemickú a podobne. Ak pôsobíme silou na objekt, meníme jeho energiu.Táto energia je použitá buď na prácu objektu, alebo na jeho zrýchlenie. Energia, na rozdiel od pohybu (vektorová veličina), nemá smer. Takýmto veličinám hovoríme skalárne veličiny. V súvislosti so silami a pohybom hovoríme najmä o kinetickej (pohybovej) energii, potenciálnej energii a energii strún (energia elastických materiálov). Energiu nie je možné cítiť dotykom alebo inak vnímať, je to len niečo, prostredníctvom čoho si vysvetľujeme, ako sa veci okolo nás dejú. Energia sa meria v jouloch.

S pohybom a jeho vysvetlením súvisí premena potenciálnej energie na kinetickú. Ak sa predmet pohybuje, hovoríme, že má kinetickú energiu. Potenciálna energia je „uskladnená“ v objektoch a jej veľkosť závisí od samotného objektu, ale aj od toho, kde a ako je umiestnený. Klasickým príkladom potenciálnej energie je snaha zdvihnúť tehlu. Keď sa tehla nachádza na zemi, má určité množstvo potenciálnej energie. Keď tehlu zdvíhame, vyvíjame na tehlu určitú silu, vynakladáme prácu. Táto vynaložená práca pridala tehle k jej potenciálnej energii ďalšiu energiu. Čím vyššie ju vynesieme, tým viac energie jej pridáme. Keď tehlu z výšky pustíme, tehla môže svojou energiou pôsobiť na iné objekty, napríklad môže niečo rozbiť. To znamená, že tehla, ktorú sme vyniesli do výšky, a tam ju držíme, má väčšiu potenciálnu energiu ako tehla, ktorá leží na zemi.

Práca

Práca vo fyzikálnom zmysle slova sa deje vtedy, keď sila, ktorou pôsobíme na objekty spôsobuje ich pohyb. Množstvo vykonanej práce tak získame, ak vynásobíme vynaloženú silu vzdialenosťou, o akú sa objekt pohol (W = F.d). Práca sa meria teda v newton-metroch, čo predstavuje to isté ako jouly. To znamená, že jednotka práce a energie je tá istá. Sila a práca nie sú to isté. Napríklad, ak držíme vo vystretej ruke tehlu, postupne sa nám bude zdať tehla ťažšia a ťažšia. Na udržanie tehly vynakladáme určitú silu, avšak, keďže sa tehla nehýbe, nevykonávame žiadnu prácu. Keď sa nám ruky unavia a tehlu položíme a znovu zdvihneme, vykonávame prácu. Menšiu prácu vykonávame keď tehlu pokladáme a väčšiu, keď ju zdvíhame. Aj napriek tomu, že dráha, ktorú tehla prejde pri pokladaní a zdvíhaní je tá istá, pri zdvíhaní musíme použiť väčšiu silu (pôsobiť proti pôsobeniu gravitačnej sily), a preto je aj výsledná práca väčšia pri zdvíhaní ako pri pokladaní tehly. Tým, že pojem práca sa používa aj v bežnej hovorovej reči, je dôležité odlíšiť fyzikálnu veličinu od bežne používaného termínu práca.

Trenie

Trenie je sila, ktorá spomaľuje pohyb kĺzajúceho sa objektu. Trenie sa vyskytuje všade tam, kde sa dostávajú do kontaktu dva objekty. Trecia sila pôsobí vždy presne opačným smerom ako je smer pohybu kĺzania objektu. Ak chceme zastaviť auto na červený signál na semafore, auto zastavuje v dôsledku trenia bŕzd (brzdových platničiek, kotúčov) o pohybujúce sa kolesá. Ak bežíme dolu kopcom po asfaltovej ceste a chceme zastaviť, tak sa nám to podarí vďaka treniu topánok o asfalt. Ak je však asfalt mokrý, prípadne je na ňom tenká riedka vrstvička blata, zastaviť sa nám tak dobre nepodarí. Podobne je to aj s pohybom auta na vozovke. Na suchej vozovke pôsobí vysoké trenie, na mokrej je trenie menšie, a preto má auto dlhšiu brzdnú dráhu. Ak sa nachádzajú kolesá v tenkej vrstve vody, môže sa stať, že strácajú kontakt s asfaltom (trenie sa stráca, lebo koleso nie je v kontakte s vozovkou, a tak nemožno hovoriť o trení) a brzdenie je neúčinné – vtedy hovoríme o aquaplaningu.

Veľkosť trenia medzi dvoma povrchmi závisí od toho, akou silou sú tlačené dva povrchy k sebe a do akej miery sú povrchy drsné. Trenie pôsobí proti akémukoľvek pohybu. Je to odpor, ktorý sa prejavuje vtedy, keď sa dva povrchy o seba trú.Žiaden povrch nie je perfektne hladký. Drobné priehlbinky alebo výčnelky, a samozrejme aj tie väčšie, na drsnejších povrchoch vzájomne do seba zapadajú, tým vzniká trenie. Okrem toho, na styk dvoch povrchov často pôsobia aj fyzikálno-chemické interakcie molekúl dvoch vzájomne sa trených povrchov.

Meranie trecej sily

Trenie (treciu silu) je možné merať. Jej veľkosť závisí od materiálov, ktoré sa po sebe kĺžu. Napríklad betón na betóne má vysoký koeficient trenia. Koeficient trenia vyjadruje to, ako ľahko sa objekt pohybuje v porovnaní s iným objektom po určitom povrchu.Ak je koeficient vysoký, znamená, že medzi materiálmi je vysoké trenie. Kým betón má vysoký koeficient trenia, napríklad teflón má nízky koeficient trenia pri všetkých materiáloch. Ešte nižší koeficient trenia majú naše kĺby. Pri trení vzniká teplo. Množstvo vzniknutého tepla závisí od veľkosti trecej sily. To znamená, že viac tepla vzniká pri trení materiálov s vysokým koeficientom trenia. Niekedy tento jav vieme využiť (napríklad šúchaním dlaní o seba si ich dokážeme zahriať), ale väčšinou spôsobuje trenie nežiaduci vznik tepla. Napríklad rôzne komplexné stroje, akými je motor auta v sebe obsahujú veľa súčastí, ktoré keď pracujú, tak sa o seba trú. Toto trenie(okrem súčastí ako sú brzdy) sa v motoroch snažíme čo najviac znížiť. Okrem toho, že priamym trením kovových súčastí o seba sa samotné súčiastky môžu opotrebovávať, vzniká trením aj veľké množstvo tepla, ktoré môže spôsobiť lokálne roztiahnutie súčiastok, ktoré sa do seba potom môžu zaseknúť. Na znižovanie trenia preto používame rôzne postupy. Ak je trenie veľmi veľké, okrem tepla je možné pozorovať iskrenie (napríklad pri používaní kotúčovej píly, pozri obrázok, alebo pri náhlom brzdení vlaku na koľajniciach).

Obrázok 23: Kotúčová píla

Znižovanie trenia

Niekedy trenie potrebujeme a niekedy sa, naopak, snažíme treniu zabrániť. Dobrým príkladom je fungovanie kolesa alebo gule. V tomto prípade ide o zmenu trenia pri posúvaní na zmenu trenia pri gúľaní. Toto trenie má vždy menšiu hodnotu. Ich tvar spôsobuje, že sa kotúľajú (neposúvajú sa), čo spôsobuje znižovanie trenia. Tento princíp dobre funguje napríklad už jednoduchým podkladaným guľatých brvien pod ťažký náklad, ale aj montovaním rôznych kolies na osi upevnených voľne na náklade. Prepracovanejším nápadom je guľôčkové ložisko. Medzi dva povrchy, na styku ktorých chceme znížiť trenie, vložíme sústavu guľôčok z dostatočne pevného materiálu. Povrchy sa v princípe netrú, lebo pri pohybe jedného o druhý sa guľôčky otáčajú a trenie dvoch plôch je tak výrazne znížené. Na princípe guľôčkového ložiska pracujú aj niektoré hračky, napríklad fidget spinner(pozri obrázok).

Na zníženie trenia sa pomerne často používajú mazacie látky.Sú to tekuté až polotekuté látky, ktoré vyplnia drobné nerovnosti v povrchoch, a tým sa dve plochy vzájomne k sebe pohybujú ľahšie, trenie je znížené. Mazacie látky sú tekuté, musia však mať väčšiu viskozitu, aby z dvoch plôch nestiekli.Problémom je, že mnohé látky majú vhodné vlastnosti na zníženie trenia, ak majú izbovú teplotu, avšak zahrievaním strácajú svoju viskozitu, sú tekutejšie a z rozhrania trených povrchov veľmi rýchlo (aj samotným pohybom objektov) unikajú (napríklad bravčová masť). Preto nie je jednoduché nájsť náhradu za mazacie látky, ktoré sa používajú profesionálnym spôsobom (napríklad vazelína).

Obrázok 24: Guľôčkové ložisko, fidget spinner

Ďalším spôsobom, pomocou ktorého je možné znížiť trenie je zmena materiálov, ktoré sú pri trení v kontakte. Napríklad oceľ sa pohybuje s veľmi nízkym trením na ľade. Ak ešte znížime kontaktnú plochu (vytvoríme akési ostrie, napríklad v prípade konštrukcie korčúľ), tak sa trenie týchto dvoch povrchov výrazne zníži. Naopak, ak nechceme, aby sa nám na chodníku šmýkalo, používame obuv s gumovou podrážkou. Pri trení gumy a asfaltu vzniká veľké trenie, a preto je táto obuv na pohyb, pri ktorom potrebujeme trenie využívať, veľmi vhodná. Ako bolo spomínané, trenie znižuje efektivitu strojov stratou vynakladanej sily (a teda stratou energie). Okrem toho sa pri trení vytvára teplo, ktoré sa zo stroja musí odvádzať. Nie všetky efekty trenia sú však nežiadané. Trenie napríklad umožňuje znížiť rýchlosť bicykla, auta, umožňuje nám chodiť, behať, ale aj písať na papier.

Odpor vzduchu

Trecia sila vzniká len pri trení pevných látok. Avšak pohybom v plynoch a kvapalinách (v tekutinách) sa samotný pohyb objektu spomaľuje v dôsledku odporu týchto látok voči pohybujúcemu sa objektu. Ak je tou tekutinou, v ktorej sa objekt pohybuje vzduch, hovoríme o odpore vzduchu. Odpor vzduchu spôsobuje napríklad to, že asteroid pri vstupe do zemskej atmosféry spôsobuje na styku meteoritu s atmosférou stlačenie molekúl vzduchu, keďže sa pohybuje veľkou rýchlosťou. Toto stlačenie spôsobí zahrievanie vzduchu a tiež samotného meteoritu. Ak je meteorit malý, tak vplyvom tohto tepla môže v atmosfére aj zhorieť.

Obrázok 25: Odpor vzduchu

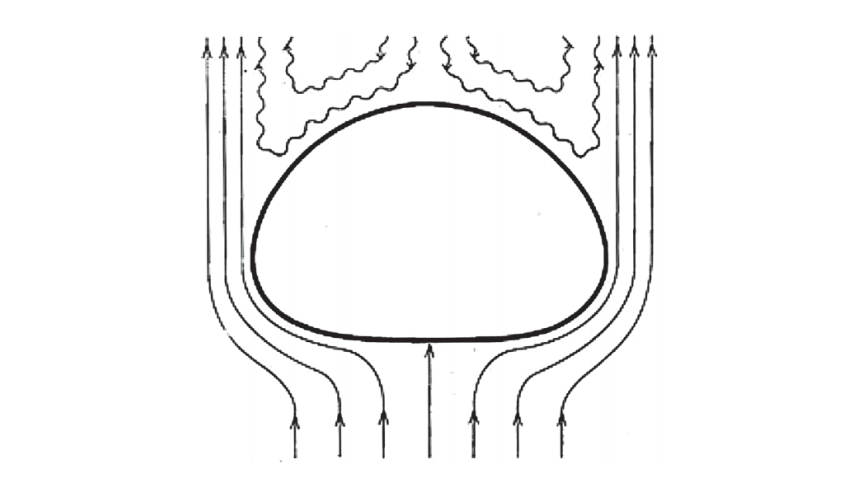
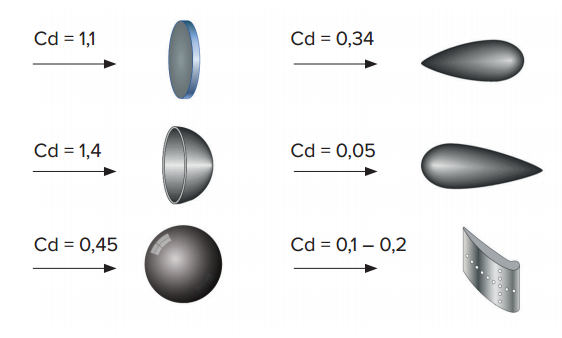
Odpor vzduchu využívame napríklad pri konštrukcii padákov. Naopak, odpor vzduchu potrebujeme znížiť, ak chceme, aby sa vo vzduchu objekty pohybovali čo najrýchlejšie, s čo najmenšou vynakladanou silou na zrýchlenie – napríklad v prípade konštrukcie lietadiel, ale aj áut a lodí. Pri konštrukcii týchto zariadení sa využívajú tzv. princípy aerodynamiky– pohybu v tekutinách(kvapalinách a plynoch). Napríklad nové modely karosérií áut sú testované vo veternom tuneli, kde sa meria odpor vzduchu, ktorý vzniká pri pohybe auta proti prúdu vzduchu. Aj preto majú autá práve taký tvar ako majú. Na obrázku sú uvedené príklady hodnôt odporu vzduchu pri rôznych telesách pohybujúcich sa vo vzduchu. Z uvedeného je zrejmé aj to, prečo má kvapka vody práve taký tvar, aký má. Keďže voda je kvapalná a môže meniť svoj tvar, pri páde z výšky mení tvar na základe toho, ako pôsobí odpor vzduchu na kvapku a výsledný tvar predstavuje ten, ktorý preniká vzduchom najľahšie (odpor vzduchu je najmenší).

Obrázok 26: Hodnoty odporu vzduchu pri rôznych telesách

Kyvadlo

Kyvadlo je tvorené závažím a špagátom, drôtom, reťazou alebo tyčou, ktorá je uchytená v pevnom bode a umožňuje závažiu kmitať z jednej strany na druhú. Keď sa závažie nachádza presne pod pevným bodom, hovoríme, že je v rovnovážnej polohe, nehýbe sa. Ak silou spôsobíme, že závažie kyvadla sa pohne do určitej strany, kyvadlo bude kmitať tam a späť v princípe donekonečna. Reálne kyvadlo postupne spomaľuje, a to najmä kvôli tomu, že neexistuje pevný bod bez trenia a taktiež sa kyvadlo pohybuje v prostredí vzduchu (tekutiny), ktorý spôsobuje odpor (pôsobí proti pohybu kyvadla) a postupné spomaľovanie kyvadla. Po rozkývaní kyvadla sa závažie dostáva do určitej maximálnej polohy. Uhol medzi špagátom v rovnovážnej a maximálnej polohe nazývame amplitúdou kmitu. Čas, ktorý potrebuje kyvadlo na vykonanie jedného celého kmitu nazývame doba kmitu. Doba kmitu závisí najmä od veľkosti gravitačnej sily, ktorá na závažie pôsobí. Z toho dôvodu to isté kyvadlo má menšiu periódu kmitu (kmitá rýchlejšie) na zemských póloch, lebo na kyvadlo pôsobí o niečo väčšia gravitačná sila ako na rovníku.

Zaujímavé je skúmanie toho, čo ovplyvňuje (aké premenné, vlastnosti kyvadla) to, ako rýchlo kyvadlo kmitá. Vzhľadom na konštrukciu kyvadla je možné brať do úvahy nasledujúce vlastnosti (premenné): dĺžku závesu (špagátu), hmotnosť závažia a uhol, z ktorého kyvadlo pri rozkývaní spúšťame. Experimentálnym skúmaním vplyvu týchto premenných je možné získať údaje uvedené v tabuľke. V pokusoch 1 až 5 bola postupne zvyšovaná hmotnosť závažia kyvadla. Ostatné premenné boli konštantné, sledovala sa súvislosť medzi zväčšujúcou sa hmotnosťou závažia a časom kmitu. Zo získaných údajov je zrejmé, že zvyšovanie hmotnosti závažia nemá efekt na rýchlosť kmitania kyvadla. To znamená, že rovnako rýchlo kmitá ľahšie aj ťažšie kyvadlo. V pokusoch 6 – 9 je hmotnosť kyvadla zachovaná rovnaká (0,2 kg), aj uhol spúšťania kyvadla je rovnaký (15°). Experimentálnou premennou je dĺžka závesu kyvadla. Týmto spôsobom je možné zistiť, či rýchlosť kmitania kyvadla závisí od dĺžky špagátu, na ktorom je závažie zavesené. Na rozdiel od hmotnosti závažia z uvedených výsledkov vyplýva, že dĺžka špagátu má efekt na rýchlosť kmitania kyvadla. Čím je špagát dlhší, tým pomalšie kyvadlo kmitá. Existuje teda priama súvislosť medzi rýchlosťou kmitania kyvadla a dĺžkou závesu (špagátu). Posledné štyri výsledky objasňujú súvislosť rýchlosti kmitania kyvadla so zmenou uhla, z ktorého kyvadlo spúšťame. Hmotnosť kyvadla a dĺžka závesu zostávajú konštantné, meníme len uhol, z ktorého kyvadlo spúšťame. Z výsledkov je zrejmé, že uhol spúšťania nemá vplyv na rýchlosť kývania kyvadla. Výsledkom všetkých meraní je, že na rýchlosť kmitania kyvadla má vplyv len dĺžka závesu kyvadla.

**Tabuľka 1:** Rýchlosť kmitania kyvadla pri zmene premenných
Číslo pokusu	Hmotnosť závažia	Dĺžka špagátu	Uhol kmitu	Čas kmitu
1.	0,02	0,4	15	1,25
2.	0,05	0,4	15	1,29
3.	0,1	0,4	15	1,28
4.	0,2	0,4	15	1,24
5.	0,5	0,4	15	1,26
6.	0,2	0,6	15	1,56
7.	0,2	0,8	15	1,79
8.	0,2	1,0	15	2,01
9.	0,2	1,2	15	2,19
10.	0,2	0,4	10	1,27
11.	0,2	0,4	20	1,29
12.	0,2	0,4	25	1,25
13.	0,2	0,4	30	1,26

Foucaultovo kyvadlo

Prvé kyvadlá sa používali na meranie časových úsekov a tiež na zisťovanie blížiaceho sa zemetrasenia dávno pred definovaním teórie kyvadiel známym vedcom Galileom Galileim.Práve jemu sa oficiálne pripisuje objav kyvadla. Prvý sa pokúsil o vysvetlenie toho, ako a prečo kyvadlá kmitajú. Práve spôsob, akým sa kyvadlo hýbe sa považuje za jeden z prvých dôkazov toho, že Zem rotuje okolo vlastnej osi. Aby sa rotácia Zeme na pohybe kyvadla prejavila, potrebujeme skonštruovať veľmi veľké kyvadlo, ktoré je zavesené na pevnom bode s maximálne zníženým trením. Takémuto zariadeniu hovoríme aj Foucaultovo kyvadlo, podľa francúzskeho fyzika Léona Foucaulta, ktorý prvýkrát kyvadlo skonštruoval(v Paríži v roku 1851), aby ním dokázal rotáciu Zeme okolo vlastnej osi.

Ak rozkývame kyvadlo pozdĺž čiary na zemi, každým jedným kmitom sa po veľmi malých kúskoch kyvadlo vychýli z pôvodného smeru. Respektíve, nie je to kyvadlo, ktoré sa vychýli, ale Zem, ktorá rotuje. Aby bol tento pohyb kyvadlom zvýraznený, pôvodne kreslilo kyvadlo čiary do piesku nasypaného pod kyvadlom. Piesok bol neskôr nahradený doštičkami, ktoré sú rozostavené pod kyvadlom v kruhu. Ak by Zem nerotovala, kyvadlo by zhodilo len dve oproti stojace doštičky. Keďže sa ale Zem otáča okolo vlastnej osi, kyvadlo postupne zhadzuje ďalšie a ďalšie doštičky rozmiestnené v kruhu. Čas, za ktorý zhodí kyvadlo všetky doštičky nazývame kyvadlovým dňom. Tento časový úsek je rôzny na rôznych častiach Zeme.

Foucaultovo originálne kyvadlo malo 28 kg ťažké závažie, ktoré viselo na 67 metrov dlhom závese. Takéto kyvadlo sa vychýlilo z pôvodného smeru asi o 11,3° za jednu hodinu, takže do pôvodnej polohy sa dostalo za približne 31,8 hodín. Na zemských póloch sa akékoľvek kyvadlo vráti do svojej pôvodnej polohy presne za 24 hodín, pričom na severnom póle rotuje kyvadlo v smere hodinových ručičiek a na južnom póle proti smeru hodinových ručičiek.

Aby sa rotácia Zeme na Foucaultovom kyvadle skutočne prejavila, kľúčové je to, ako bude kyvadlo spustené. Amplitúda by mala byť maximálne 20 stupňov, pričom spustené Foucaultovo kyvadlo nie by malo byť bez pôsobenia rôznych bočných síl. Na spustenie sa napríklad používa prepálenie špagátu, ktorý drží závažie kyvadla vychýlené. Napodobeniny Foucaultovho kyvadla sa nachádzajú v mnohých prírodovedných múzeách. Keďže na kyvadlá pôsobí odpor vzduchu, postupne by spomaľovali, preto sa do konštrukcií kyvadiel montujú rôzne mechanizmy, ktoré zabezpečujú ustálené kmitanie kyvadla. Napríklad sa pohyb kyvadla zrýchľuje elektromagnetickým pôsobením na závažie, a to tak, aby sa presne vyrovnalo spomaľovanie v dôsledku odporu vzduchu. Jednoduchším spôsobom, ktorý je tiež pomerne často využívaný je opätovné spustenie kyvadla.

Obrázok 27: Foucaultovo kyvadlo