



Silou a pohybem se zabývá mechanika, která je považována za klíčovou oblast fyziky. Je možné tvrdit, že vše ve vesmíru se pohybuje. Může jít i jen o velmi drobný pohyb a velmi, velmi pomalý pohyb, ale děje se. Fyzika pohybu se zabývá zejména silami.Pokud chceme způsobit pohyb objektu nebo změnit jeho pohyb, potřebujeme na objekt působit silou. Žádná změna pohybu se neděje sama od sebe, vždy jde o změnu působení sil na daný objekt. Změna působení sil na objekt může způsobit změnu směru jeho pohybu a/ nebo změnu rychlosti jeho pohybu.
Při změně pohybu je třeba brát v úvahu rychlost, zrychlení a hmotnost objektu. Rychlost objektu vyjadřuje to, jakou dráhu objekt projde za určitý čas. Zrychlení vyjadřuje to, jak se zvětšila rychlost pohybu objektu za určitý čas. Pohyb objektů závisí i na jejich hmotnosti. Hmotnost vyjadřuje množství materiálu, kterým je objekt tvořen (vyjadřuje se v kilogramech, gramech). Takže například pohybující se auto má určitou rychlost, zrychlení a hmotnost. Tyto vlastnosti je třeba brát v úvahu při hodnocení jeho pohybu, zejména při snaze změnit jeho pohyb, například při snaze auto zastavit.
Rychlost i zrychlení mají vektorový charakter. To znamená, že mají svou velikost i směrování. Nejjednodušeji se to vysvětluje na zobrazení pomocí šipek. Šipka určuje směr rychlosti a její délka určuje to, jak rychle se objekt v určitém směru pohybuje. Zrychlení je také vektorová veličina. Objekt zrychluje, když zrychlení i rychlost mají stejný směr. Pokud mají směr opačný, objekt zpomaluje. Specifické je tzv. konstantní zrychlení. Zrychlení je konstantní v případech, kdy na objekt působí konstantní síla.Příkladem konstantního zrychlení je tzv. gravitační zrychlení, které je výsledkem působení konstantní gravitační síly Země. Gravitace působí na objekt konstantní silou směrem do centra planety Země. Gravitační síla Země se zmenšuje se zvětšující se vzdáleností od povrchu planety. Také je zajímavé si uvědomit, že gravitace jiných planet se od gravitace Země odlišuje, protože planety mohou mít větší nebo menší hmotnost než planeta Země. Proto předměty při pádu zrychlují jinak na Zemi a jinak na jiných planetách.
Pokud vynásobíme rychlost objektu jeho hmotností, dostaneme další vektorovou veličinu - hybnost. Hybnost má vždy stejný směr jako rychlost. V principu tato veličina vyjadřuje to, jak těžké je zastavit určitý pohybující se objekt. Pokud například běží člověk rychlostí 10 kilometrů za hodinu a váží 50 kg, jeho hybnost je 500 kg.m/s. Pokud letí míč, který váží 1 kilogram rychlostí 10 kilometrů za hodinu, v případě, že nás trefí, zraní nás méně než míč, který váží více a/nebo se pohybuje rychleji. Hybnost takového míče je 10 kg · m/s.
Z uvedeného, okrem iného, vyplýva, že aj veľmi drobné objekty (ľahké) nás môžu zraniť viac ako veľké objekty (ťažké), ak je ich rýchlosť veľmi veľká. Typickým príkladom je náboj vystrelený zo zbrane. Náboj sám o sebe je veľmi ľahký a ak by ho do nás niekto len hodil, tak nám vôbec neublíži. Práve hybnosť spôsobuje zranenia, pričom veľká hybnosť náboja je z nepomerne väčšej časti spôsobená rýchlosťou náboja, nie jeho hmotnosťou. Platí to aj naopak. Aj veľmi pomaly sa pohybujúce, ale ťažké predmety nám môžu ublížiť, napríklad ak si pricvikneme prsty pod skriňu, ktorú sťahujeme.
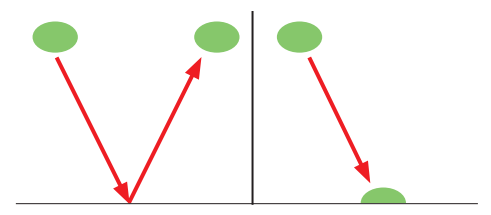
Hybnost objektu představuje kinetickou energii objektu. Ta se zachovává i tehdy, pokud takový objekt narazí na překážku a odrazí se od ní. Platí to však jen tehdy, pokud jde o ideálně pružný objekt. Při nárazu objektu s ideální pružností se mění hybnost objektu, ale jen ve směru jejího působení. Velikost hybnosti zůstává stejná, mění se pouze směr, kterým se objekt pohybuje. V principu ideální pružnost neexistuje, známe jen objekty s různě velkou pružností. Čím méně pružný materiál je, tím více kinetické energie se při odrazu ztrácí. Ideálně pružný a ideálně nepružný dopad objektu a vliv dopadu na hybnost jsou zobrazeny na obrázku. Jelikož ideálně pružné a nepružné materiály neexistují, nelze tento jev demonstrovat, je však možné pozorovat rozdíly mezi předměty s velmi vysokou a velmi nízkou pružností, například pingpongový míček a plastelínu. Pokud hodíme na zem kuličku plastelíny, ta zůstane deformovaná ležet na podlaze. Část kinetické energie plastelíny se změnila na teplo (plastelína se pádem zahřeje) a zvuk (vibrace na podlaze a zvukové vlny ve vzduchu). Jelikož po dopadu je rychlost nulová, i hybnost je nulová. Kinetická energie nezmizela, jen se proměnila na jinou formu energie. Čím pružnější je materiál, tím více energie zůstává ve formě pohybové energie, například pingpongový míček se na rozdíl od plastelíny od překážky odrazí.
Na základě dlouhodobého studia pohybu byly postupně definovány základní principy pohybu a změn v pohybu, které také nazýváme pohybovými zákony. Formuloval je Isaac Newton a jsou tři. Kromě těchto základních tří pohybových zákonů známe i další, které se vážou na specifické případy pohybů, jako je pohyb rychlostí blížící se rychlosti světla a také pohyb v mikrosvětě, na úrovni atomů. Z toho vyplývá, že v těchto specifických situacích přestávají Newtonovy pohybové zákony platit.
První pohybový zákon hovoří o tom, že pohybující se objekt setrvává v pohybu ve stejném směru a stejnou rychlostí, dokud na něj nepůsobí nějaká síla.To znamená, že pokud kopneme do míče, ten bude letět konstantní rychlostí nekonečně daleko, dokud na něj nebude působit jiná síla. I přesto, že na první pohled není tento zákon v souladu s realitou, platí to absolutně. Po kopnutí do míče působí na pohybující se míč síly, které způsobují jeho zpomalování a následně i pád. Jde například o gravitační sílu Země, která táhne míč směrem dolů (tato síla působí na míč i pokud leží v klidu), ale i tření o vzduch, ve kterém se míč pohybuje.
Druhý pohybový zákon hovoří o tom, že čím větší hmotnost objekt má, tím větší sílu bude třeba vynaložit na to, aby se pohyb objektu zrychlil(F = m · a). Mimo jiné to znamená, že čím silněji kopnete do míče, tím dále poletí. Pokud tedy působíme stejnou silou na dva objekty s různou hmotností, více zrychlí objekt, který má větší hmotnost.
Třetí pohybový zákon hovoří o tom, že každá akce vyvolává stejně velkou, ale opačně působící reakci. To znamená, že v každém okamžiku existují dvě síly vzájemně na sebe působící. V příkladu s míčem to znamená, že když vynaložíme sílu na kopnutí do míče, tak i míč působí stejně velkou silou na naši nohu, jen opačným směrem. Cítíme to zejména tehdy, když do míče kopneme prsty. Síla, kterou míč působí na naši nohu může být tak velká (závisí na tom, jak silně do míče kopneme), že způsobí zlomení prstu. Viditelněji se třetí pohybový zákon projevuje například při střílení z děla (ale i z jiných střelných zbraní). Výbuchem je dodána síla dělové kouli, která je kanónem v určitém směru vystřelená. Avšak stejně velkou silou působí i dělová koule na kanón. Kanón se pohne opačným směrem než vystřelená dělová koule, ne však tak rychle jako samotná koule a to proto, že kanón je mnohem těžší a na jeho zrychlení je proto nutné vynaložit větší sílu, než na zrychlení mnohem lehčí dělové koule.
Existují dva pohledy na výsledný, pozorovaný pohyb objektů. První pohled řeší pohyb jako přímočaré přemisťování, přičemž rychlost přemisťování může být konstantní, ale vlivem sil působících ve směru pohybu nebo v přesně opačném směru se může objekt pohybovat pomaleji nebo rychleji. Složitějším je pohyb, při kterém objekt mění směr svého pohybu. Například rotující objekty nebo míč hozený šikmým vrhem. I při takových pohybech musí na objekt působit síla, avšak ta nepůsobí ve směru pohybu objektu (případně proti směru pohybu), ale pod určitým úhlem.
Na vysvětlení toho, proč se věci kolem nás dějí tak, jak se dějí, používáme pojem energie. Známe různé formy energie, například sluneční, atomovou, elektrickou, chemickou a podobně. Pokud působíme silou na objekt, měníme jeho energii.Tato energie je použita buď na práci objektu nebo na jeho zrychlení. Energie, na rozdíl od pohybu (vektorová veličina), nemá směr. Takovým veličinám říkáme skalární veličiny. V souvislosti se silami a pohybem mluvíme zejména o kinetické (pohybové) energii, potenciální energii a energii strun (energie elastických materiálů).Energii nelze cítit dotykem nebo jinak vnímat, je to jen něco, prostřednictvím čeho si vysvětlujeme, jak se věci kolem nás dějí. Energie se měří v joulech.
S pohybem a jeho vysvětlením souvisí přeměna potenciální energie na kinetickou. Pokud se předmět pohybuje, říkáme, že má kinetickou energii. Potenciální energie je „uskladněna“ v objektech a její velikost závisí na samotném objektu, ale také na tom, kde a jak je umístěn. Klasickým příkladem potenciální energie je snaha zvednout cihlu. Když se cihla nachází na zemi, má určité množství potenciální energie. Když cihlu zvedáme, vyvíjíme na cihlu určitou sílu, vynakládáme práci. Tato vynaložená práce přidala cihle k její potenciální energii další energii. Čím výše ji vyneseme, tím více energie jí přidáme. Když cihlu z výšky pustíme, cihla může svou energií působit na jiné objekty, například může něco rozbít. To znamená, že cihla, kterou jsme vynesli do výšky, a tam ji držíme, má větší potenciální energii než cihla, která leží na zemi.
Práce ve fyzikálním smyslu slova se děje tehdy, když síla, kterou působíme na objekty způsobuje jejich pohyb. Množství vykonané práce tak získáme, když vynásobíme vynaloženou sílu vzdáleností, o jakou se objekt pohnul (W = F · d). Práce se tedy měří v newtonmetrech, co představuje totéž jako jouly. To znamená, že jednotka práce a energie je stejná. Síla a práce nejsou totéž.Například, pokud držíme v natažené ruce cihlu, postupně se nám bude zdát cihla těžší a těžší. Na udržení cihly vynakládáme určitou sílu, avšak, protože se cihla nehýbe, neprovádíme žádnou práci. Když se nám ruce unaví a cihlu položíme a znovu zvedneme, provádíme práci. Menší práci provádíme když cihlu pokládáme a větší, když ji zvedáme. I přesto, že dráha, kterou cihla projde při pokládání a zvedání je tatáž, při zvedání musíme použít větší sílu (působit proti působení gravitační síly), a proto je i výsledná práce větší při zvedání než při pokládání cihly. Tím, že pojem práce se používá také v běžné hovorové řeči, je důležité odlišit fyzikální veličinu od běžně používaného termínu práce.
Tření je síla, která zpomaluje pohyb klouzajícího se objektu. Tření se vyskytuje všude tam, kde se dostávají do kontaktu dva objekty. Třecí síla působí vždy přesně opačným směrem než je směr pohybu klouzání objektu. Pokud chceme zastavit auto na červený signál na semaforu, auto zastavuje v důsledku tření brzd (brzdových destiček, kotoučů) o pohybující se kola. Jestliže běžíme dolů kopcem po asfaltové cestě a chceme zastavit, tak se nám to podaří díky tření bot o asfalt. Pokud je však asfalt mokrý, případně je na něm tenká řídká vrstvička bláta, zastavit se nám tak dobře nepodaří. Podobně je to i s pohybem auta na vozovce. Na suché vozovce působí vysoké tření, na mokré je tření menší, a proto má auto delší brzdnou dráhu. Pokud se kola nachází v tenké vrstvě vody, může se stát, že ztrácejí kontakt s asfaltem (tření se ztrácí, protože kolo není v kontaktu s vozovkou, a tak nelze hovořit o tření) a brzdění je neúčinné - tehdy mluvíme o aquaplaningu.
Velikost tření mezi dvěma povrchy závisí na tom, jakou silou jsou tlačeny dva povrchy k sobě a do jaké míry jsou povrchy drsné. Tření působí proti jakémukoliv pohybu. Je to odpor, který se projevuje tehdy, když se dva povrchy o sebe třou.Žádný povrch není perfektně hladký. Drobné prohlubně nebo výstupky, a samozřejmě i ty větší, na drsnějších površích vzájemně do sebe zapadají, tím vzniká tření. Kromě toho, na styk dvou povrchů často působí i fyzikálně-chemické interakce molekul dvou vzájemně se třených povrchů.
Tření (třecí sílu) je možné měřit. Její velikost závisí na materiálech, které se po sobě kloužou. Například beton na betonu má vysoký koeficient tření. Koeficient tření vyjadřuje to, jak snadno se objekt pohybuje ve srovnání s jiným objektem po určitém povrchu. Pokud je koeficient vysoký, znamená to, že mezi materiály je vysoké tření. Zatímco beton má vysoký koeficient tření, například teflon má nízký koeficient tření u všech materiálů. Ještě nižší koeficient tření mají naše klouby.
Při tření vzniká teplo. Množství vzniklého tepla závisí na velikosti třecí síly. To znamená, že více tepla vzniká při tření materiálů s vysokým koeficientem tření. Někdy tento jev umíme využít (například dotykem dlaní o sebe si je dokážeme zahřát), ale většinou způsobuje tření nežádoucí vznik tepla. Například různé komplexní stroje, jakými je motor auta v sobě obsahují mnoho součástí, které když pracují, tak se o sebe třou. Toto tření (kromě součástí jako jsou brzdy) se v motorech snažíme co nejvíce snížit. Kromě toho, že přímým třením kovových součástí o sebe se samotné součástky mohou opotřebovávat, vzniká třením i velké množství tepla, které může způsobit lokální roztažení součástek, které se pak do sebe mohou zaseknout. Na snižování tření proto používáme různé postupy. Pokud je tření velmi velké, kromě tepla je možné pozorovat jiskření (například při používání kotoučové pily, viz obrázek, nebo při náhlém brzdění vlaku na kolejích).

Někdy tření potřebujeme a někdy se naopak snažíme tření zabránit. Dobrým příkladem je fungování kola nebo koule. V tomto případě jde o změnu tření při posouvání na změnu tření při kutálení. Toto tření má vždy menší hodnotu. Jejich tvar způsobuje, že se kutálejí (neposouvají se), což způsobuje snižování tření. Tento princip dobře funguje například již jednoduchým podkládáním kulatých břeven pod těžký náklad, ale i montováním různých kol na ose upevněných volně na nákladu. Propracovanějším nápadem je kuličkové ložisko. Mezi dva povrchy, na styku kterých chceme snížit tření, vložíme soustavu kuliček z dostatečně pevného materiálu. Povrchy se v principu netřou, neboť při pohybu jednoho o druhý se kuličky otáčejí a tření dvou ploch je tak výrazně snížené. Na principu kuličkového ložiska pracují i některé hračky, například fidget spinner (viz obrázek).
Na snížení tření se poměrně často používají mazací látky. Jsou to tekuté až polotekuté látky, které vyplní drobné nerovnosti v površích, a tím se dvě plochy vzájemně k sobě pohybují snadněji, tření je sníženo. Mazací látky jsou tekuté, musí však mít větší viskozitu, aby ze dvou ploch nestekli.Problémem je, že mnohé látky mají vhodné vlastnosti pro snížení tření, pokud mají pokojovou teplotu, avšak zahříváním ztrácejí svoji viskozitu, jsou tekutější a z rozhraní třených povrchů velmi rychle (i samotným pohybem objektů) unikají (například vepřové sádlo). Proto není jednoduché najít náhradu za mazací látky, které se používají profesionálním způsobem (například vazelína).

Dalším způsobem, pomocí kterého lze snížit tření je změna materiálů, které jsou při tření v kontaktu. Například ocel se pohybuje s velmi nízkým třením na ledě. Pokud ještě snížíme kontaktní plochu (vytvoříme jakési ostří, například v případě konstrukce bruslí), tak se tření těchto dvou povrchů výrazně sníží. Naopak, pokud nechceme, aby se nám na chodníku klouzalo, používáme obuv s gumovou podrážkou. Při tření gumy a asfaltu vzniká velké tření, a proto je tato obuv na pohyb, při kterém potřebujeme tření využívat, velmi vhodná. Jak bylo zmíněné, tření snižuje efektivitu strojů ztrátou vynakládané síly (a tedy ztrátou energie). Kromě toho se při tření vytváří teplo, které se ze stroje musí odvádět. Ne všechny efekty tření jsou však nežádané. Tření například umožňuje snížit rychlost kola, auta, umožňuje nám chodit, běhat, ale i psát na papír.
Třecí síla vzniká pouze při tření pevných látek. Jenže pohybem v plynech a kapalinách (v tekutinách) se samotný pohyb objektu zpomaluje v důsledku odporu těchto látek vůči pohybujícímu se objektu. Pokud je tou tekutinou, ve které se objekt pohybuje vzduch, mluvíme o odporu vzduchu. Odpor vzduchu způsobuje například to, že asteroid při vstupu do zemské atmosféry způsobuje na styku meteoritu s atmosférou stlačení molekul vzduchu, protože se pohybuje velkou rychlostí. Toto stlačení způsobí zahřívání vzduchu a také samotného meteoritu. Pokud je meteorit malý, tak vlivem tohoto tepla může v atmosféře i shořet.
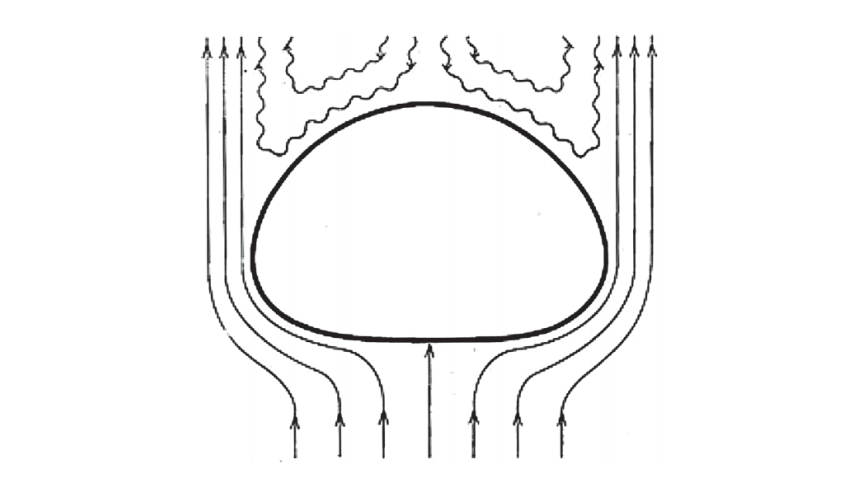
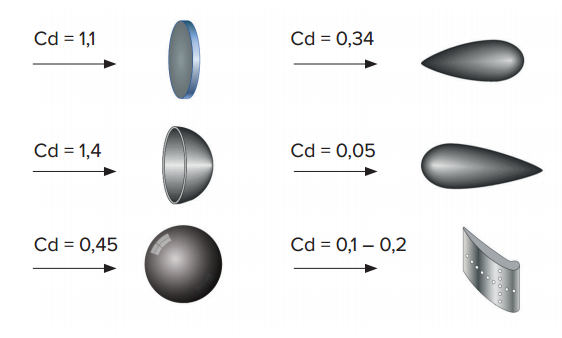
Odpor vzduchu využíváme například při konstrukci padáků.Naopak, odpor vzduchu potřebujeme snížit, pokud chceme, aby se ve vzduchu objekty pohybovaly co nejrychleji, s co nejmenší vynakládanou silou na zrychlení – například v případě konstrukce letadel, ale i aut a lodí. Při konstrukci těchto zařízení se využívají tzv. principy aerodynamiky - pohybu v tekutinách(kapalinách a plynech). Například nové modely karoserií aut jsou testovány ve větrném tunelu, kde se měří odpor vzduchu, který vzniká při pohybu auta proti proudu vzduchu. I proto mají auta právě takový tvar jaký mají. Na obrázku jsou uvedeny příklady hodnot odporu vzduchu u různých těles pohybujících se ve vzduchu. Z uvedeného je zřejmé i to, proč má kapka vody právě takový tvar, jaký má. Protože voda je kapalná a může měnit svůj tvar, při pádu z výšky mění tvar na základě toho, jak působí odpor vzduchu na kapku a výsledný tvar představuje ten, který proniká vzduchem nejsnáze (odpor vzduchu je nejmenší).
Kyvadlo je tvořeno závažím a provázkem, drátem, řetězem nebo tyčí, která je uchycena v pevném bodě a umožňuje závaží kmitat z jedné strany na druhou. Když se závaží nachází přesně pod pevným bodem, říkáme, že je v rovnovážné poloze, nehýbe se. Pokud silou způsobíme, že závaží kyvadla se pohne do určité strany, kyvadlo bude kmitat tam a zpět v principu donekonečna. Reálné kyvadlo postupně zpomaluje, a to zejména kvůli tomu, že neexistuje pevný bod bez tření a taktéž se kyvadlo pohybuje v prostředí vzduchu (tekutiny), který způsobuje odpor (působí proti pohybu kyvadla) a postupné zpomalování kyvadla. Po rozkývání kyvadla se závaží dostává do určité maximální polohy. Úhel mezi provázkem v rovnovážné a maximální poloze nazýváme amplitudou kmitu. Čas, který potřebuje kyvadlo na provedení jednoho celého kmitu nazýváme doba kmitu.Doba kmitu závisí zejména na velikosti gravitační síly, která na závaží působí. Z toho důvodu totéž kyvadlo má menší periodu kmitu (kmitá rychleji) na zemských pólech, neboť na kyvadlo působí o něco větší gravitační síla než na rovníku.
Zajímavé je zkoumání toho, co ovlivňuje (jaké proměnné, vlastnosti kyvadla) to, jak rychle kyvadlo kmitá. Vzhledem ke konstrukci kyvadla je možné brát v úvahu následující vlastnosti (proměnné): délku závěsu (provázku), hmotnost závaží a úhel, ze kterého kyvadlo při rozkývání spouštíme. Experimentálním zkoumáním vlivu těchto proměnných je možné získat údaje uvedené v tabulce. V pokusech 1 až 5 byla postupně zvyšována hmotnost závaží kyvadla. Ostatní proměnné byly konstantní, sledovala se souvislost mezi zvětšující se hmotností závaží a časem kmitu. Ze získaných údajů je zřejmé, že zvyšování hmotnosti závaží nemá efekt na rychlost kmitání kyvadla. To znamená, že stejně rychle kmitá lehčí i těžší kyvadlo. V pokusech 6 – 9 je hmotnost kyvadla zachována stejná (0,2 kg), i úhel spouštění kyvadla je stejný (15°). Experimentální proměnnou je délka závěsu kyvadla. Tímto způsobem je možné zjistit, zda rychlost kmitání kyvadla závisí na délce provázku, na kterém je závaží zavěšeno. Na rozdíl od hmotnosti závaží z uvedených výsledků vyplývá, že délka provázku má efekt na rychlost kmitání kyvadla. Čím je provázek delší, tím pomaleji kyvadlo kmitá. Existuje tedy přímá souvislost mezi rychlostí kmitání kyvadla a délkou závěsu (provázku).Poslední čtyři výsledky objasňují souvislost rychlosti kmitání kyvadla se změnou úhlu, ze kterého kyvadlo spouštíme. Hmotnost kyvadla a délka závěsu zůstávají konstantní, měníme pouze úhel, ze kterého kyvadlo spouštíme. Z výsledků je zřejmé, že úhel spouštění neovlivňuje rychlost kývání kyvadla. Výsledkem všech měření je, že na rychlost kmitání kyvadla má vliv pouze délka závěsu kyvadla.
| Číslo pokusu | Hmotnost závaží | Délka provázku | Úhel kmitu | Čas kmitu |
|---|---|---|---|---|
| 1. | 0,02 | 0,4 | 15 | 1,25 |
| 2. | 0,05 | 0,4 | 15 | 1,29 |
| 3. | 0,1 | 0,4 | 15 | 1,28 |
| 4. | 0,2 | 0,4 | 15 | 1,24 |
| 5. | 0,5 | 0,4 | 15 | 1,26 |
| 6. | 0,2 | 0,6 | 15 | 1,56 |
| 7. | 0,2 | 0,8 | 15 | 1,79 |
| 8. | 0,2 | 1,0 | 15 | 2,01 |
| 9. | 0,2 | 1,2 | 15 | 2,19 |
| 10. | 0,2 | 0,4 | 10 | 1,27 |
| 11. | 0,2 | 0,4 | 20 | 1,29 |
| 12. | 0,2 | 0,4 | 25 | 1,25 |
| 13. | 0,2 | 0,4 | 30 | 1,26 |
První kyvadla se používala k měření časových úseků a také na zjišťování blížícího se zemětřesení dávno před definováním teorie kyvadel známým vědcem Galileem Galileim. Právě jemu se oficiálně připisuje objev kyvadla. První se pokusil o vysvětlení toho, jak a proč kyvadla kmitají. Právě způsob, jakým se kyvadlo hýbe se považuje za jeden z prvních důkazů toho, že Země rotuje kolem vlastní osy. Aby se rotace Země na pohybu kyvadla projevila, potřebujeme zkonstruovat velmi velké kyvadlo, které je zavěšené na pevném bodě s maximálně sníženým třením. Takovému zařízení říkáme i Foucaultovo kyvadlo, podle francouzského fyzika Léona Foucaulta, který poprvé kyvadlo zkonstruoval(v Paříži v roce 1851), aby jím dokázal rotaci Země kolem vlastní osy.
Pokud zhoupneme kyvadlo podél čáry na zemi, každým jedním kmitem se po velmi malých kouscích kyvadlo vychýlí z původního směru. Respektive, není to kyvadlo, které se vychýlí, ale Země, která rotuje. Aby byl tento pohyb kyvadlem zvýrazněn, původně kreslilo kyvadlo čáry do písku nasypaného pod kyvadlem. Písek byl později nahrazen destičkami, které jsou rozestaveny pod kyvadlem v kruhu. Kdyby u Země nedocházelo k rotaci, kyvadlo by shodilo jen dvě oproti stojící destičky. Jelikož se ale Země otáčí kolem vlastní osy, kyvadlo postupně shazuje další a další destičky rozmístěné v kruhu. Čas, za který shodí kyvadlo všechny destičky nazýváme kyvadlovým dnem. Tento časový úsek je různý na různých částech Země.
Aby se rotace Země na Foucaultovém kyvadle skutečně projevila, klíčové je to, jak bude kyvadlo spuštěno. Amplituda by měla být maximálně 20 stupňů, spuštění by mělo být bez působení různých bočních sil. Na spuštění se například používá propálení provázku, který drží závaží kyvadla vychýlené. Napodobeniny Foucaultova kyvadla se nacházejí v mnoha přírodovědných muzeích. Jelikož na kyvadla působí odpor vzduchu, postupně by zpomalovaly, proto se do konstrukcí kyvadel montují různé mechanismy, které zajišťují ustálené kmitání kyvadla. Například se pohyb kyvadla zrychluje elektromagnetickým působením na závaží, a to tak, aby se přesně vyrovnalo zpomalování v důsledku odporu vzduchu. Jednodušším způsobem, který je také poměrně často využíván je opětovné spuštění kyvadla.
