Arbeitsauftrag 10

Da wir eine bereits aufgeschriebene Skala haben (unten), können wir diese mit den Schülerinnen und Schülern in der Aktivität als ein Werkzeug für die Unterstützung der Untersuchung verstehen. Daher ist es gut, sich zuerst der Konstruktion dieser Grafik und seiner Verwendung zu widmen, damit die Schüler die Bedeutung verstehen. Sobald eine Forschungsfrage gestellt wird (Wie schräg muss der Ball geschossen werden, damit er so weit wie möglich fliegt?), diskutiert die Lehrerin oder der Lehrer mit den Schülerinnen und Schülern, wie der optimale Winkel am besten gemessen werden kann. Angesichts der Entwicklung eines Wissenschaftsprozesses ist es wichtig, dass Raum bleibt um eigene Verfahren zu entwerfen. Wenn eine der Ideen ausreichend durchdacht ist, kann sie auch verwendet werden.

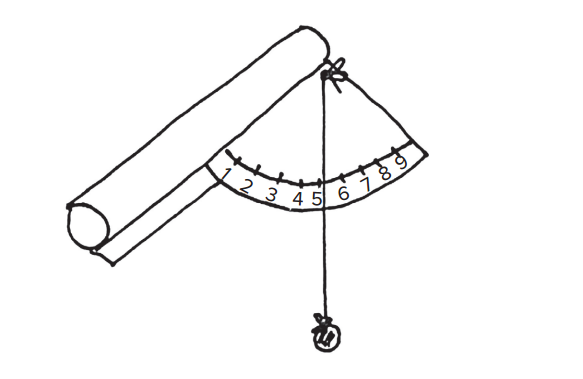
Wenn die Schülerinnen und Schüler keinen eigenen Vorschlag haben, kann der Lehrer oder die Lehrerin die Erstellung eines vereinfachten Instrumentes zur Messung des Winkels zum Abwerfen der Objekte vorschlagen. Zuerst wird aus einem dicken Papier ein Viertelkreis herausgeschnitten, an dessen Rand in regelmäßigen Abständen die Zahlen von 1 bis 8 aufgetragen worden sind (wie von 10° bis 90°, also im rechten Winkel). Es ist am besten, wenn die Lehrerin oder der Lehrer diese Viertelkreise für die Schülerinnen und Schüler vorbereitet, so dass die regelmäßigen Striche der gemessenen Winkel bereits zur Verfügung stehen. Alternativ kann in der Klasse auch eine Vorlage zum Zeichnen der Skala ausgeteilt werden. Ein neues Papier kann nun eng eingerollt und daran die Winkelskala fixiert werden. In der Ecke des Winkelmessers wird ein Loch gemacht und ein Faden mit kleinem Gewicht daran festgebunden. Die Schnur ist der Richtungsanzeiger. Die Schüler können ein Objekt betrachten und den Winkel bestimmen, mit dem sie (wie schräg) schießen, wenn sie mit dem Gewicht zielen.

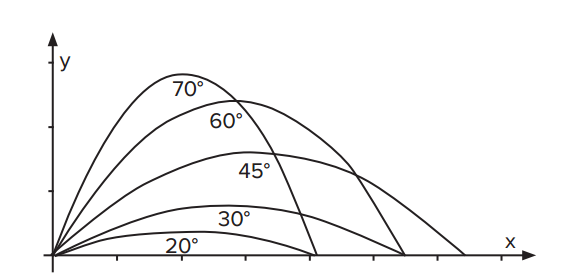
Wenn die Schüler mit der Verwendung des Richtungsmessers vertraut sind, können sie eine Forschungsfrage beantworten: Wie schräg muss der Ball gefeuert werden, damit er so weit wie möglich fliegt? Für die Entwicklung von Ideen über Wissenschaft ist es jedoch wichtig, die Schülerinnen und Schüler überprüfen zu lassen, ob das Diagramm in Arbeitsauftrag 10 wirklich auch zeigt, wohin die Objekte fallen, wenn wir sie in verschiedene Richtungen werfen. Der Arbeitsauftrag führt dazu, dass die Informationen aus dem Diagramm zu abgelesen und interpretiert werden. Die Daten im Diagramm sind in Graden angegeben, es ist sehr einfach, diese Grade in Zahlen auf einer eigenen Skala zu konvertieren (z. B. 20° = 2; 30° = 3, 90° = 9, usw.).